(In Proakis & Salehi unless otherwise noted)
Read Sections 5.1, 5.2
Do 5.1, 5.2, 5.3, 5.5, 5.9
Functions and application to WBFM, WBPM
Read Chapter 4
Do 4.4, 4.5, 4.20
Read 3.5, Review "Appendix 3A, page 149,
Read Chapter 4
Do 3-A (not in text), 4.1, 4.2
Hints on problem 4.1
--For part one you should leave the integral
unsolved. The "sine integral" is a tabulated
function with no known analytic solution. Just
show the integral in your solution.
Some details of the Sine Integral can be found here
A well known and heavy authority on topics like this is
the handbook by Abramowitz and Stegun. Available in
the John and Louise Hulst Library (you will see that this
handbook is literally heavy) or electronically. See
especially Section 5.2 if you like these details.
Hint: You should pay attention to units. The
modulation index is always dimensionless (e.g.
radians). The deviation constant, kf is usually in
Hz/V in our text. (Some texts use rad/(s-V))
--For part three, delete the word "content" from
the question. Since the frequency and phase
of the R.F. signal vary only slowly relative to
the carrier you can assume m(t) = 0 to find the
power and you will get the same result as if
m(t) were not zero.
--For part four use Carson's Rule.
--Typo: In problem 4.2 part two replace fd
with kf. The units on fd will be rad/volt and the
units on fd will be Hz/volt.
methods of modulation and demodulation
Read Sections 3.2.4, 3.3
Do 3.16, 3.17
Review 3.2.1, 3.2.2, Read Section 3.2.3
Do 3.11
AM Modulation, DSB-SC, DSB-LC
Read 2.4, 2.5, 2.8, 3.1, 3.2 up to 3.2.3
Do 3.1, 3.3, 3.5, 3.14, and note errata on
pages 151 and 152, also. . .
Prove that the F.T. is linear, also. . .
Use a computer to plot Eq. 3.2.6 (page 127).
Let mn(t) = cos(2πfmt) and let a = 0.75, Ac = 10,
fm = 440 Hz, and fc = 100 kHz. Turn that case
in for a grade, but use your computer code to
explore. What happens if a > 1?
What happens as fc is lowered toward fm?
Be sure your plots have enough samples. You
should have at least 10 samples per cycle of
of cos(2πfct) and you should plot at least one
cycle of mn(t).
Use a computer for the plots for 3.3.
(Problem 2.50 was originally and mistakenly a part of
this assignment. It was removed on 3/03/2014.)
Read Section 2.3
Do evaluate the following integral:
![Integral from minus inf.
to inf. of {[2exp(-5t) +sin(10(pi)t)]delta(t)}dt](Integral_1.png)
Also evaluate the convolution
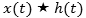
where
and
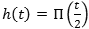
and do these from the textbook: 2.41,
2.43 part b only, 2.44, 2.46, 2.50, 2.51
Review Ch. 2 Section 2.2.
Do 2.37, 2.39, 2.42, and also find
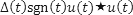where sgn is the signum function and u is the unit step function.
The delta represents the unit triangle function
and the star represents convolution.
(In class on 2/7 Problem 2.46 was moved to the next
assignment.)
Reading: Ch. 2, Review Section 2.1, read 2.2
Do 2.7, 2.24, 2.34
(As per discussion in class on 1/29, problems 2.37 and
2.39 were delayed to the next assignment.
Read: Ch 2 Sec. 1.4, Ch.2 through Sec. 2.1
Do (p. 101) 2.1 (all parts), 2.5, 2.6, 2.16.
Use a computer to make the plots for 2.1.
Octave or Matlab are recommended.
Here is a m-file to get you started.
Hint: At the command line in Octave or Matlab
type, "help sign" [enter]. Also try
"help addpath", "help help" and "help exit".
Note errata on pages 29 and 42, and 101, 102.
Read Chapter 1.
(There is nothing to turn in.)