#
(In Proakis & Salehi unless otherwise noted)
Do 5.3, 5.5, 5.9, 5.10, 5.11 parts 1 and 2 only.
Hints on 5.11
Part 3) You can't use Eq. 5.1.11 (Why?)
Use techniques discussed in class.
Part 4) The integral you encounter is not too
hard. What is d/dy(exp(y2/2
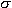 2))?
2))? Part 5) You can use Eq. 5.1.11.
As discussed in class on Wed. 4/28, parts 3,
4 and 5 of problem 5.11 have been deleted from
this problem set. We have run out of time.
Do 4.4, 4.5
Do this problem (not in the text): 3-A
Do 4.1
Hints on problem 4.1
--For part one you should leave the integral
unsolved. The "sine integral" is a tabulated
function with no known analytic solution. Just
show the integral in your solution.
Some details of the Sine Integral can be found here
A well known but heavy authority on topics like this is
the handbook by Abramowitz and Stegun. Available in
the John and Louise Hulst Library (you will see that this
handbook is literally heavy) or electronically. See
especially Section 5.2 if you like these details.
You should also pay attention to units. The
modulation index, is always dimensionless. The
The deviation constant, kf is usually in Hz/V in
our text.
--For part three, delete the word "content" from
the question. Since the frequency and phase
of the R.F. signal vary only slowly relative to
the carrier you can assume m(t) = 0 to find the
power and you will get the same result as if
m(t) were not zero.
--For part four use Carson's Rule.
(The solution to 3-A is not posted.)
Do 3.16, 3.18, 3.24
(The solution to 3.18 is not posted)
Do 3.14.
Review problem 2.51 which shows that
multiplication in the time domain is equivalent
to convolution in the frequency domain. This
is a useful theorem.
Read 3.1, 3.2
Do 3.1, 3.3, 3.5
Note errata on problems 3.1, 3.3, 3.5.
Do 2.26, 2.46.1, 2.46.2, 2.51
Hint: A direct application of the Fourier
Transform's analysis equation to problems
2.46.1 and 2.46.2 results in a challenging
integral. A lookup table of integrals would
be a potential way to get a correct answer,
but these integrals are usually not given in
the types of lookup tables included in a
typical calculus textbook. Instead, one can
use the table on page 81 of our text as a
lookup table of integrals. Application of the
properties of Fourier Transforms is also
helpful.

L. Euler
Do 2.34.2, 2.34.6, 2.39.5, 2.39.11, 2.39.12
Note publisher's errata on 2.39, page 113,
lines 6 through 17.
In general, the subscript on x(t) should match the
problem part number.
Hint for 2.39.5: x5(t) is a very simple signal given
in a messy form.
Hint for 2.39.11 and 2.39.12: Use a corollary
of Euler's formula to expess the signal as a
complex exponential. Exponentials are easier
to integrate than trigonometric functions.
(See the end of this page on Euler's formula.)
Do 2.5, 2.6, 2.7, 2.24, 2.34.3
Note errata on Problem 2.6.
Do 2.2.1, 2.2.2, 2.2.3
Do (page 105) 2.1.1, 2.1.3, 2.1.5, 2.1.7, 2.1.9
Use a Matlab script ("m-file") to make the plots.
Write the problem statement into the script as
a comment. Import the script and the plot into
a word processor file to control fomatting and
to print.
Note errata on page 31 and errata on page 44.