#
(In Proakis & Salehi unless otherwise noted)
(Study for the final exam.)
at
10 AM
Do 5.11, 5.12 except omit part 4, 5.40
Hints on 5.11
Part 3) You can't use Eq. 5.1.11 (Why?)
Use techniques discussed in class.
Part 4) The integral you encounter is not too
hard. What is d/dy(exp(y2/2
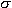 2))?
2))? Part 5) You can use Eq. 5.1.11.
Hints on 5.12
Part 1) You can use Eq. 5.1.11.
Part 2) Find the CDF first.
Part 4) Omit.
Do 5.3, 5.5, 5.9, 5.10
On Thursday, 4/17, two problems (5.11, and
5.23) were deleted from this assignment since
we have not covered those topics in class yet.
Do P4.20, 5.1, 5.2
Do 4.1, 4.4, 4.5, and this problem:
Find the image frequency for radio station WNAX
which broadcasts at 570 kHz. Assume the
receiver has an IF frequency of 455 kHz and
that the local oscillator is at a frequency
above that of the station.
Hints on problem 4.1
--For part one you should leave the integral
unsolved. The "sine integral" is a tabulated
function with no known analytic solution. Just
show the integral in your solution.
(Some details of the Sine Integral can be found here
A well known but heavy authority on topics like this is
the handbook by Abramowitz and Stegun. Available in
the John and Louise Hulst Library (you will see that this
handbook is literally heavy) or electronically. See
especially Section 5.2 if you like these details.
You should also pay attention to units. The
modulation index, is always dimensionless. The
The deviation constant, kf is usually in Hz/V in
our text.
--For part three, delete the word "content" from
the question. Since the frequency and phase
of the R.F. signal vary only slowly relative to
the carrier you can assume m(t) = 0 to find the
power and you will get the same result as if
m(t) were not zero.
--For part four use Carson's Rule.
Do 3.14, 3.16, 3.24
Reveiw the "Modulation Theorem" on page 72-74.
Do 3.1, 3.3, 3.5
Do 2.26, 2.34.2, 2.46.1, 2.46.2, 2.51
Hint: Both 2.46.1 and 2.46.2 can be done by
applying the analysis equation directly to x(t)
but note that the table on page 81 can be used
as a lookup table of integrals and the
properties of the Fourier transform (linearity,
time shift, etc.) can also be used to simplify
your work.
Do 2.34.3, 2.34.5, 2.39.5, 2.39.11, 2.39.12
Note publisher's errata on 2.39,
page 113 lines 6 through 17.
In general, the subscript on x(t) should match
the problem part number.
On 2/04 problem 2.46.1 was moved from this
assignment to PS #4, as per class discussion.
Do 2.6, 2.7, 2.24
Do (page 105) 2.1.1, 2.1.3, 2.1.5, 2.1.7, 2.1.9
2.2.1, 2.2.2, 2.2.3, 2.5
Use Matlab to make the plots. Import the plots
to a word processor file to control formatting.
This Problem Set was originally due on 1/21.
On 1/21 the due date was extended to 1/23.
Note added on 1/30/08: Errata on page 31.