(In Proakis & Salehi unless otherwise noted)
Read Ch 4 Sec 4.3, 4.4
Note textbook errata on page 163.
Note textbook errata on page 187, Prob. 4.20.
Review Ch 3 Sec. 3.4, 3.5, 3.6,
Read Ch 4 Sec 4.1, 4.2
Errata on Problem 4.2 discovered 12/04.
Superheterodyne tuning, image freq.
Read Ch 3 Sec. 3.2.3, 3.2.4, 3.4, 3.5
Ch 2 Sec. 2.6, slides
Read Ch 3 Sec. 3.2.2, 3.2.3, Ch 2 Sec. 2.6
Read Ch 3 Sec. 3.1, 3.2.1, 3.2.2
On problem 3.3, Let f0 = 5 Hz and let A = 1 V.
Use a computer to make your plots. It is too
tedious to achieve the needed plot accuracy
when plotting by hand. Matlab, Desmos, and
many other programs can do this task for you.
Here is a hint in Matlab code that provides
one way to express the message signal m1(t):
m1 = (2*t).*(u(t) - u(t - 0.5)) + ...
(-2*t).*(u(t - 0.5) - u(t - 1.5)) + ...
(2*t).*(u(t - 1.5) - u(t - 2.0))
When you repeat the problem for DSB-LC make
use of Equation 3.2.6 on page 127.
On problem 3.5, you may make your plots by
hand, but maintain good accuracy on properly
scaled axes. When you draw an impulse, make
the height of the impulse represent the area
under the impulse.
Note errata on pages 151 and 152.
Read Ch 2 Sec. 2.3
Read Ch 2 Sec. 2.2
Hints:
See all the hints for PS#5 below.
In Problem 2.39.6 the fundamental period is not
1/f0. If you doubt this statement, let f0 = 60 Hz,
for example, and plot the time-domain signal.
Then find the fundamental period by observing the
plot.
Problem 2.46.2 can be done using tables found
in your textbook, pages 78 and 79. Euler's
is also helpful in recognizing the result.
(Up to about 5:10 PM on Tu, 10/15 the list of problems
to do was erroneously the same as PS#6
Read Ch 2 Sec. 2.2
Hints:
See all the hints for PS#5 below.
Problem 2.42 is asking you to find the time-
domain dot product x(t)·y(t) and show
that it is the same as the frequency-domain dot
product of xn·yn. To do this, in the time-domain
dot product (L.H.S. of the given eq.), replace x(t)
with its equivalent from the F.S. synthesis
equation. Similarly substitute for y(t). Make sure
the two summations use different index (harmonic
number) variables such as n and k. (Not n and n.)
Integrate term-by-term. (In other words, invoke
distribution of multiplication with respect to
addition to re-order operations and move the
integration operation fully inside the
summations.) This creates a double summation
of integrals. The Fourier series coefficients xn and
yk are constants with respect to the integration.
Notice that if the two indices of summation
(harmonic numbers) are not equal, the basis
functions are orthogonal. his causes most terms
in the double-summation to be zero. The only
terms that remain non-zero occur when the
indices of summation happen to be equal. Thus
the double summation can be reduced to the
single summation given in the problem statement.
Note: On 10/08 the due date was changed from 10/08
to 10/15 to accommodate the test.
Read Ch 2 Sec. 2.2
Hints:
For problem 2.36 the author expects you to let
the basis signals equal zero outside of the
defined interval [α, α + T0].
Divide-by-zero errors are possible mistakes
when working the F.S. analysis integral. Do you
see something like (2 – n) in a denominator? Then
this solution is good only if n ≠ 2. Handle the
n = 2 case separately by substituting n = 2 early,
before the (2 – n) gets expressed in a denom.
Keep Euler's rule in mind. Remember that com-
plex exponentials can be written as cos() + jsin()
or similar trigonometric forms and vice versa.
Terms like cos(2
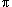n) can be reduced.cos(2
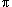n) = 1 for all n Terms like cos(
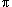n) can be reduced tocos(
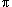n) = (–1)nSimilar maneuvers can be made with sin()
functions involving multiples of
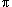.In the answer for 2.39.1, xn = 0 for most n but
not every n.
The answer for 2.39.4 for odd n can be
expressed in the form (integer)/(pn)2. Here p is
a real constant and n is the harmonic number.
If n is even but not zero, then xn equals a "special
integer." If n = 0, then xn = x0 = a rational number.
Two additional slides have been added at the
end of the slide file for 9/12. These slides
elaborate on the definition of the dot product of
two signals. These slides might be helpful in
working Problem 2.36.
Note: errata on textbook page 107, Prob. 2.38
This problem is not assigned, but an error in
this problem statement could be confusing when
working Problem 2.36. In the first integral in
the problem statement of problem 2.38 the "1"
and the "0" are interchanged from where they
should be. The integral evaluates to 0 if i ≠ j
and it evaluates to 1 if i = j
Note: In class on 9/17 prof. dDB said that Problem 2.36
was moved from PS#4 to PS#5. This finally got noted on
this web page on 9/21 at about 1:15 PM
Read Ch 2 Sec. 2.1
Read and observe Problems 2.37, 2.38 on pages
106-107. These are theorems that relate to
transforms in general. The proofs requested are
tedious (hence not assigned), but the theorems
are famous.
Read Ch 2 Sec. 2.1
Read: Ch 1 Sec. 1.4, Ch.2 through Sec. 2.1
Use a computer to make the plots for 2.1.
Octave or Matlab are recommended.
Here is a m-file to get you started.
DDB's "Toolbox" files including u.m, rect.m,
sinc.m and triangle.m can be downloaded as a
zip archive DDB_TBX.ZIP.
Hint: At the command line in Octave or Matlab
type, "help sign" [enter]. Also try
"help addpath", "help help" and "help exit".
After file rect.m is on the path-list, note
what happens when you type "help rect" in the
command window. Compare to the comments in
the source file, rect.m.
Note errata on pages 29 and 42, and 101, 102.
Read Chapter 1.
(There is nothing to turn in.)