Professor De Boer's list of
TEXTBOOK ERRATA
(last update 12/06/07)


Polking, Boggess, and Arnold
Differential Equations, 2nd Ed. ISBN 0-13-143738-0
Pearson Prentice Hall, 2006.

In addition to the errata shown here, Professor Teck-Cheong Lim at George Mason University keeps a list of errata for this text. Errata shown on his list are not repeated here.

Still more errata on this text can be found at this wiki. As of the time when this link was added to this page, errata were only listed for Chapter 2.


Additional Errata are shown below

Page 6, Problem 10
Unclear: "...the force is inversely proportional to but opposite the square of the particle's displacement from the origin."

Clear: "...the magnitude of the force is inversely proportional to the square of the particle's displacement from the origin but the direction of the force is opposite to the direction of the particle's displacement from the origin."

Page 13, Third line from the bottom.
The word "that" is obscured or jumbled.

Page 35, Exercise 23
(updated 9/11/06)

Page 145, Above Exercise 1
In the last sentence of the paragraph that starts, "For each. . ."
change, "If the equation in linear, . . ." to
"If the equation is linear, . . ."       (posted 10/10/07)

Page 145, Exercise 11
Missing units: "R(v) = –0.05v"
Correct: "R(v) = –0.05(kg/s)v"
Also add this sentence to the problem statement: "Assume that the displacement of fluid due to the immersion of the mass results in negligible floating.

(For example consider a mass where the "viscous solution" is air confined in a cylinder only slightly larger than the mass)."

(updated 10/10/07)


Page 191, about 1/3 down the page,
The statement, "When s < a, the exponent is positive and so the term involving. . ."
is incorrect.

The variables s and a are elements of the complex numbers and thus cannot be simply related as less than or greater than. The sentence should read, "When
Re{s} < Re{a}, the term involving. . ." This problem persists throughout the chapter and in the solutions given in the appendix. In every case where something like, "provided s > a" is stated, it should be "provided Re{s} > Re{a}."

Page 234, Starting about two inches from the bottom of the page
Incorrect: "We want to interchange the order . . .
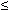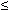                                                      0 u t < .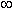
                                                                        . . . . Hence we get"

Correct: "We want to interchange the order of integration in (7.8). In doing so the integral signs with their limits are interchanged as well as the differential du and dt. After interchanging the order of integration, the upper limit of the outer integral would be t, which was the upper limit of the inner integral before changing the order of integration. Note however that after changing the order of integration,
if u > t in the outer integral, then g(t – u) = 0, (because g(x) = 0 for all x < 0) therefore the upper limit of the outer integral can be changed to ."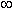

Similarly, after changing the order of integration, the lower limit of the inner integral should be 0, which was formerly the lower limit of the outer integral. However, the inner lower limit can be changed to u since g(t – u) = 0 for all t < u.

Remark: The limits of integration in Definition 7.5 (about two inches from the top of page 234) are shown as 0 to t. This is only accurate when f(t) = g(t) = 0 for all t < 0, as is assumed to be the case in the context of the type of Laplace transforms under discussion in this chapter. A general definition however has limits of
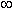– to 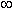. Then stipulate in Theorem 7.6 that the theorem only applies if
f(t) = g(t) = 0 for all t < 0. In this case the inner integral in Equation 7.8 would have initially been written with limits from –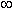 to 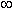. Then since f(u) = 0 for all
u < 0 the lower limit of the inner integral can be changed to 0. (The upper limit of the inner integral then is 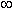with no further fuss.)

Page A-4, Section 2.5, Answer to Exercise 1 (from page 61)
Incorrect: "9.038"
Correct: "9.0238" or just "9.024"

Page A-5, Section 2.6, Answer to Exercise 27 (from page 75)
Incorrect: "ln x"     (Absolute value sign is missing.)
Correct: "ln|x|"

Page A-5, Section 2.6, Answer to Exercise 35 (from page 75)
Incorrect: x² – Cx = y²     (Absolute value sign is missing.)
Correct: y² = |x² – Cx|     (y² = |x² + Cx| is also correct since C can be
                                       positive or negative.)  (posted 10/04/06)

Page A-8, Section 4.1, Answer to Exercise 11 (from page 145)
The given answer is incorrect. The correct answer is:

2(kg)y" + 0.05(kg/s)y' + 39.2(kg/s²)y =
      19.6(kg m/s²){1 + sin[(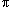 rad/s)t]}

The cos function is also acceptable in place of sin since
the problem only states "harmonic" motion. (updated 10/31/06)

Page A-10, Section 4.6. The answer to Exercise 9
The given answer is incorrect. The correct answer is:

x(t) = (1/3) + (1/3)cos²(t)
                  or
x(t) = (1/2) + (1/6)cos(2t)

Also, the answers to 1, 7, and 11 look suspicious, but I have not checked them specifically.