DORDT UNIVERSITY ENGINEERING DEPARTMENT
INTRODUCTION TO COMMUNICATION SYSTEMS—EGR 363
(Fall 2020)
Story version of PS#5
In this story version of the problem statements I shall repeat the problem statements using only words. Although there will be almost no mathematical symbolism to speed your way, perhaps you will find hints of what the equations in the problem statements mean—hints that may be hard for students to pick up on until they gain a deeper understanding of the symbolism of the equations. Problem two-point-thirty-six. Show that a set of signals comprising an set of complex exponentials has the property that for every pair of signals of different harmonics (different values of |n|) the pair is orthogonal (one signal has no projection on the other signal) and that each signal has a power of 1 W (relative to 1 Ω). For example if one signal has n = 2 and the other has n = 3 the two signals are orthogonal and each signal has power of 1 W. But this needs to be proven for any pair of harmonics having different |n|. Hint: represent one of the signals in a pair as √(1/T0)exp(j2 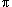 mt/T0)
and the other as mt/T0)
and the other as √(1/T0)exp(j2 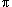 mt/T0)
where m and k are integers, possible values for n,
and |m| ≠ |k|. mt/T0)
where m and k are integers, possible values for n,
and |m| ≠ |k|.
Problem two-point-thirty-nine-point-one and also -point-four. Determine the Fourer Series expansion of the given signal. (The answer is a set of xn values. |